Is 0 An Odd Or Even Number?
In mathematics, the classification of numbers plays a crucial role in various branches of study. One of the most intriguing discussions revolves around the number 0. This article will explore the nature of 0, delving into whether it is classified as an odd or even number.
The concept of odd and even numbers is foundational in mathematics. Even numbers are those that can be divided by 2 without any remainder, while odd numbers are those that cannot. To determine the classification of 0, we must examine its properties and how it interacts with the definitions of odd and even.
This article will analyze the mathematical principles surrounding the number 0, reference reputable sources, and provide a comprehensive understanding that is accessible to readers of all backgrounds. We will conclude with a summary of our findings and invite you to engage in the discussion.
Table of Contents
- Definition of Even and Odd Numbers
- The Nature of Zero
- Is Zero an Even Number?
- Is Zero an Odd Number?
- Mathematical Properties of Zero
- Zero in Different Mathematical Contexts
- Historical Perspective on Zero
- Conclusion
Definition of Even and Odd Numbers
To comprehend whether 0 is odd or even, we must first define these two classifications:
- Even Numbers: An integer is classified as even if it can be expressed in the form of 2n, where n is an integer. This means that when an even number is divided by 2, the result is always another integer without any remainder.
- Odd Numbers: An integer is considered odd if it can be expressed as 2n + 1, where n is an integer. Odd numbers, when divided by 2, will yield a remainder of 1.
The Nature of Zero
Zero (0) is a unique number in mathematics. It serves as the additive identity, meaning that any number added to 0 remains unchanged. This property sets it apart from other integers. Moreover, zero plays a pivotal role in various mathematical operations, including multiplication and division.
To determine the classification of 0, we can apply the definitions of even and odd numbers:
- When we divide 0 by 2, the result is 0, which is an integer. Thus, it satisfies the condition for being even.
- Since 0 cannot be expressed in the form of 2n + 1, it does not meet the criteria for being odd.
Is Zero an Even Number?
Based on the definition of even numbers, we can conclude that 0 is indeed an even number. Here are some key points supporting this assertion:
- **Divisibility by 2:** 0 divided by 2 equals 0, which is an integer. Therefore, it can be expressed as 2n (with n=0).
- **Pattern of Even Numbers:** The sequence of even numbers includes ..., -4, -2, 0, 2, 4, ... This sequence clearly shows that 0 fits within the category of even integers.
- **Mathematical Consensus:** Mathematicians universally recognize 0 as an even number. This classification is consistent across various mathematical texts and educational resources.
Is Zero an Odd Number?
In contrast, let’s evaluate the claim that 0 could be an odd number:
- **Remainder Check:** When dividing 0 by 2, there is no remainder, which contradicts the requirement for odd numbers (which must leave a remainder of 1).
- **Formulation:** 0 cannot be expressed in the form of 2n + 1, as this would necessitate n to be a non-integer.
Thus, the conclusion is clear: 0 cannot be classified as an odd number.
Mathematical Properties of Zero
Understanding the properties of 0 is essential for comprehending its role in mathematics:
- **Additive Identity:** As mentioned earlier, adding 0 to any number does not change the value of that number.
- **Multiplicative Property:** Any number multiplied by 0 results in 0.
- **Zero in Equations:** Zero can be a solution to various equations, showcasing its importance in algebra and calculus.
Zero in Different Mathematical Contexts
Zero is not only important in basic arithmetic but also plays a crucial role in advanced mathematical concepts:
- Calculus: In calculus, zero is used to define limits and is critical in understanding continuity and differentiability.
- Set Theory: The empty set is represented by 0, emphasizing its significance in higher mathematics.
- Graph Theory: In graph theory, the concept of zero is fundamental in defining vertices and edges.
Historical Perspective on Zero
The history of zero is fascinating and reflects its evolution in mathematical thought:
- Ancient Civilizations: The concept of zero was developed independently by various ancient civilizations, including the Babylonians, Mayans, and Indians.
- Modern Adoption: The acceptance of zero in European mathematics emerged in the Middle Ages, largely due to translations of Arabic mathematical texts.
- Philosophical Implications: Zero has prompted philosophical debates about the nature of nothingness and existence.
Conclusion
In summary, the number 0 is unequivocally classified as an even number based on mathematical definitions and properties. It does not qualify as an odd number due to its inability to meet the necessary criteria. Understanding the nature of zero enhances our comprehension of mathematics as a whole.
We encourage you to engage with this topic further by leaving a comment below or sharing this article with others interested in mathematics. Explore our other articles for more insights!
Thank you for reading, and we hope to see you again soon!
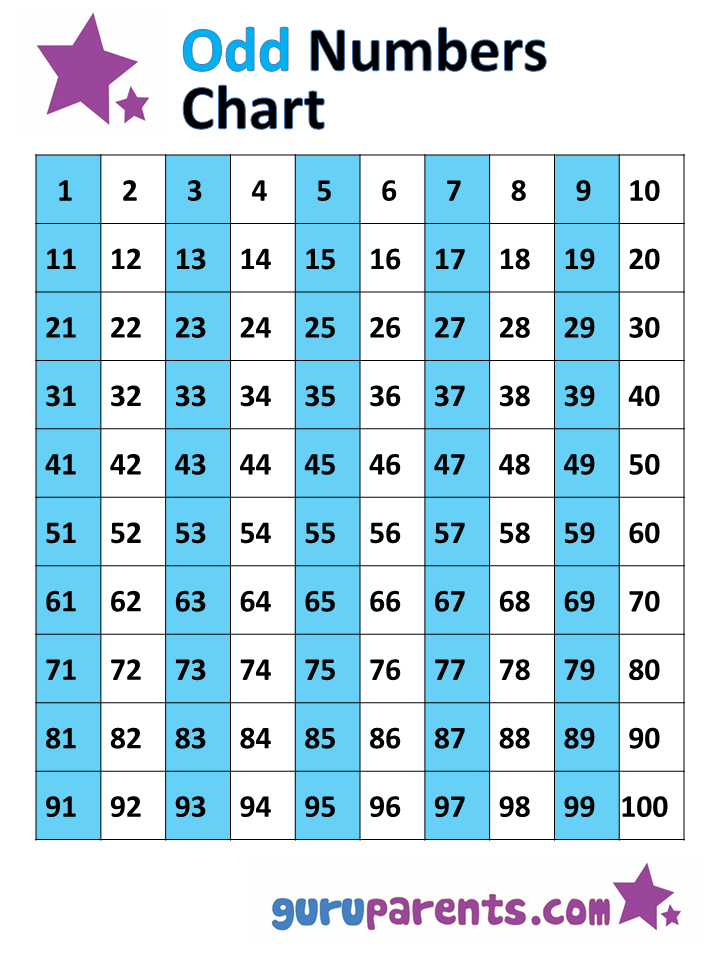
Chart Of Even And Odd Numbers
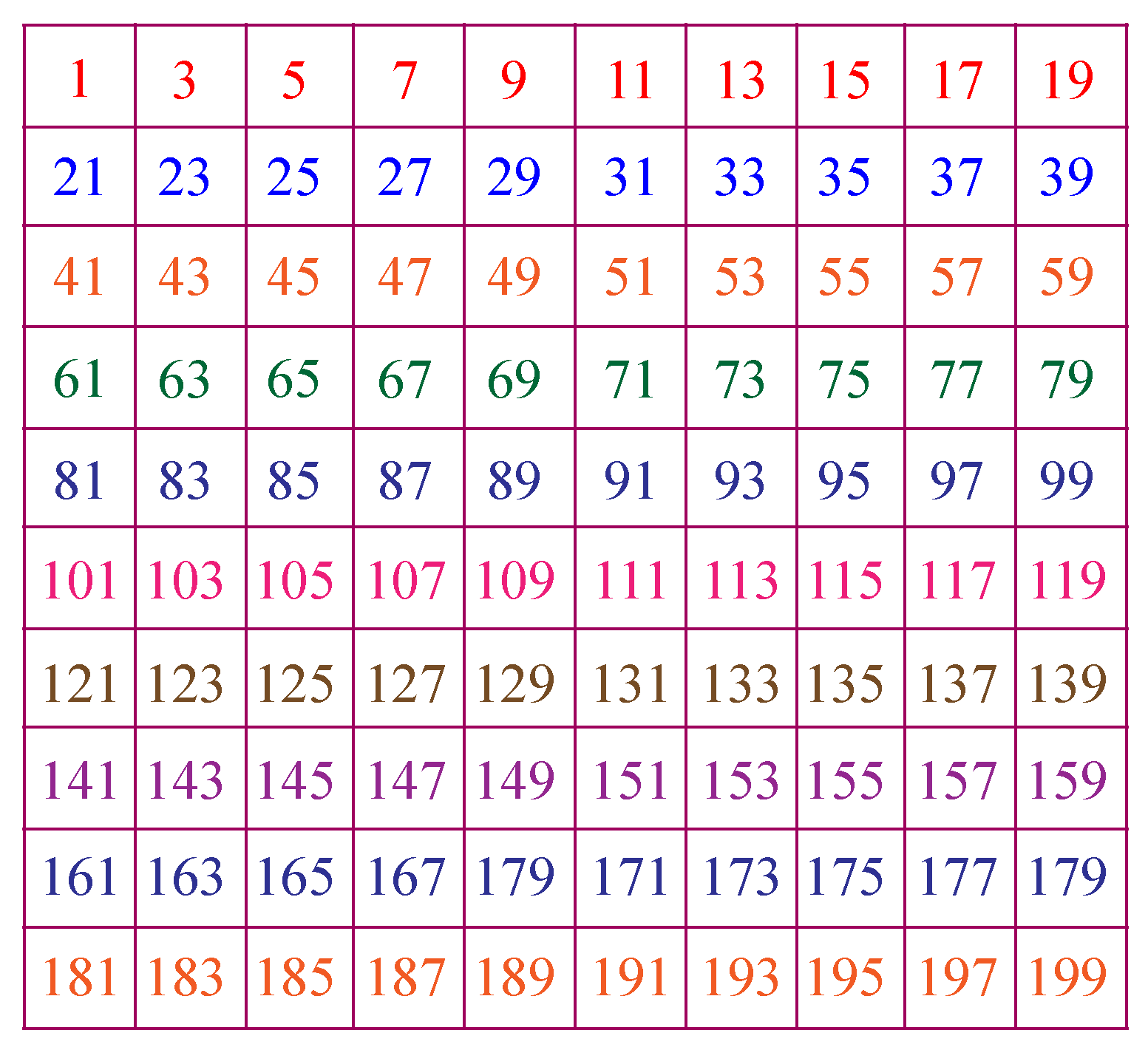
Odd Or Even Chart
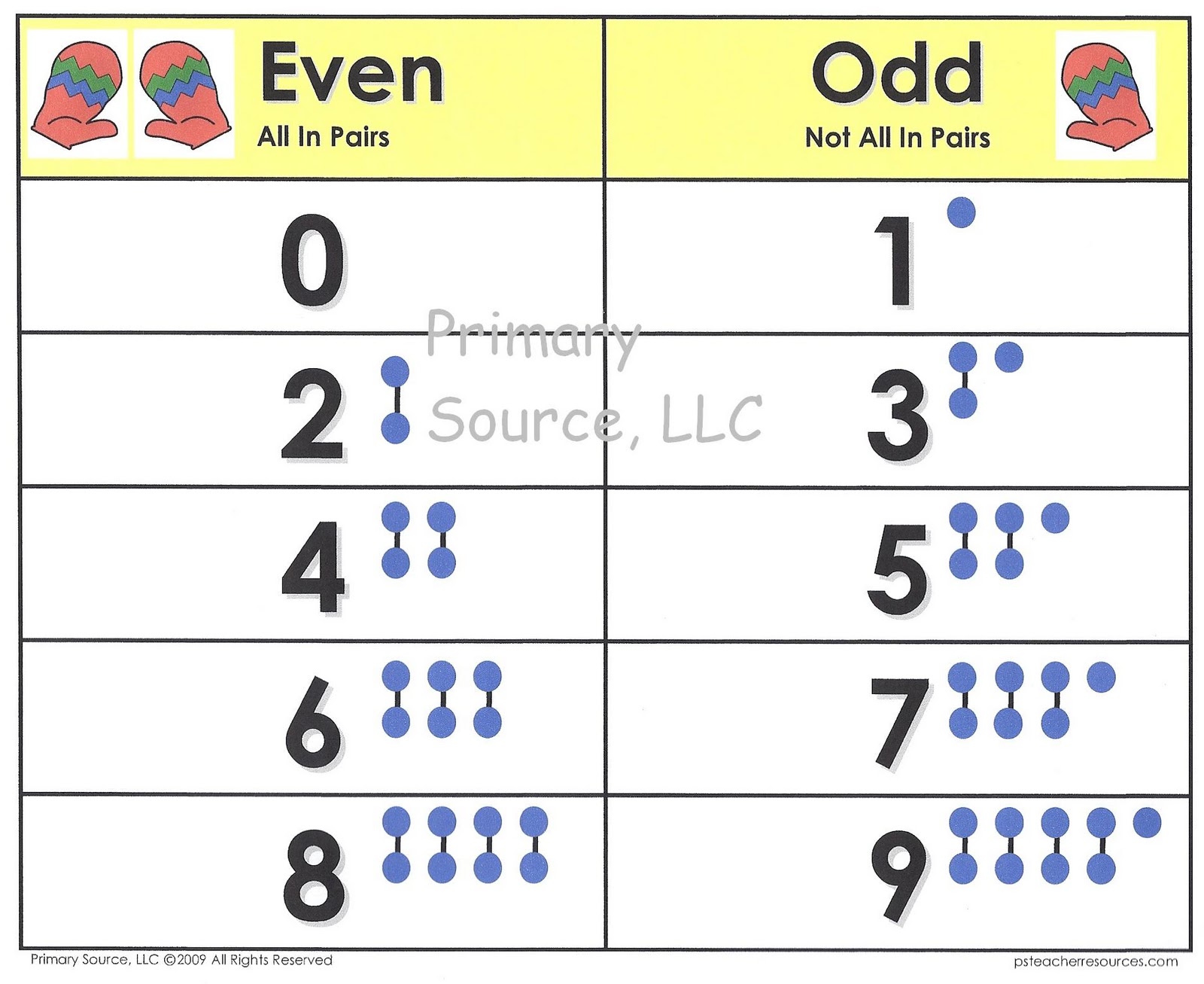
Odd Numbers And Even Number Chart For Kids